6.1 One-loop four-point example

As a simple example of how the unitarity method gives loop amplitudes, consider the one-loop amplitude with four identical helicity gravitons and a scalar in the loop [22, 23]. The product of tree amplitudes appearing in the channel unitarity cut depicted in Fig.  9 is

where the superscript s indicates that the cut lines are scalars. The h subscripts on legs indicate that these are gravitons, while the ``+'' superscripts indicate that they are of plus helicity. From the KLT expressions (10) the gravity tree amplitudes appearing in the cuts may be replaced with products of gauge theory amplitudes. The required gauge theory tree amplitudes, with two external scalar legs and two gluons, may be obtained using color-ordered Feynman diagrams and are

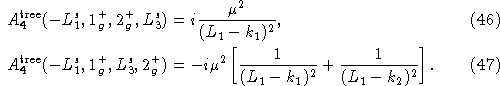
The external gluon momenta are four-dimensional, but the scalar momenta and are D -dimensional since they will form the loop momenta. In general, loop momenta will have a non-vanishing -dimensional component , with . The factors of appearing in the numerators of these tree amplitudes causes them to vanish as the scalar momenta are taken to be four-dimensional, though they are non-vanishing away from four dimensions. For simplicity, overall phases have been removed from the amplitudes. After inserting these gauge theory amplitudes in the KLT relation (10), one of the propagators cancels, leaving

For this cut, one then obtains a sum of box integrals that can be expressed as

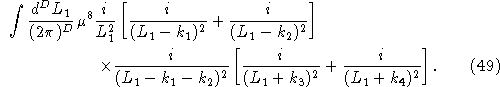
By symmetry, since the helicities of all the external gravitons are identical, the other two cuts also give the same combinations of box integrals, but with the legs permuted.

The three cuts can then be combined into a single function that has the correct cuts in all channels yielding

 

and where

 

is the box integral depicted in Fig.  11 with the external legs arranged in the order 1234. In Eq. (50) is . The two other integrals that appear correspond to the two other distinct orderings of the four external legs. The overall factor of 2 in Eq. (50) is a combinatoric factor due to taking the scalars to be complex with two physical states.

Since the factor of is of , the only non-vanishing contributions come where the from the interferes with a divergence in the loop integral. These divergent contributions are relatively simple to obtain. After extracting this contribution from the integral, the final D =4 result for a complex scalar loop, after reinserting the gravitational coupling, is

 

in agreement with a calculation done by a different method relying directly on string theory [55]. (As for the previous expressions, the overall phase has been suppressed.)

  

Figure 11: The one-loop box integral. Each internal line in the box corresponds to one of the four Feynman propagators in Eq. (51).

This result generalizes very simply to the case of any particles in the loop. For any theory of gravity, with an arbitrary matter content one finds:

 

where is the number of physical bosonic states circulating in the loop minus the number of fermionic states. The simplest way to demonstrate this is by making use of supersymmetry Ward identities [71, 104, 20], which provide a set of simple linear relations between the various contributions showing that they must be proportional to each other.

Perturbative Quantum Gravity and its Relation to Gauge Theory Zvi Bern http://www.livingreviews.org/lrr-2002-5 © Max-Planck-Gesellschaft. ISSN 1433-8351 Problems/Comments to livrev@aei-potsdam.mpg.de